三入力カルノー図 3 input Karnaugh map

三入力でのカルノー図の作り方を説明します。

以下の様な真理値表があったとします。

この場合、先ずFが１になる場所に着目します。

さらに以下のような図を描きます。

ここに真理値表の数値を当てはめていきます。

当てはめていく数値はF=1の値です。

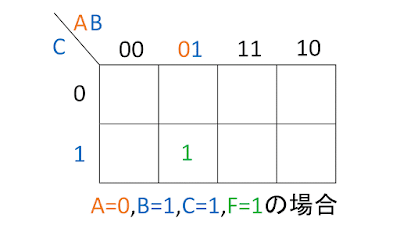
例えば、A=0,B=1,C=1,F=1の場合だと以下の様になります。

またA=1,B=0,C=1,F=1の場合だと

の様になります。

こうやってF=1の場所をすべて埋めます。

すると結果的には下図の様になります。

そしてこの四角の中の隣接する1同士を２の累乗に

相当する個数づつで囲います。

2の累乗とは1,2,4,8,16,・・・のことです。

この時四角の中の1すべて囲われるようにします。

今回は全ての１を2個づつの組で囲えました。

場合によっては当然4個や8個の組で囲える場合もあります。

また端同士は隣接するものと見做します。

この囲った組全てについてひとつづつ見ていきます。

先ず、紫で囲った部分についてみていきます。

この様に囲ったものの中で必ず0又は１になる部分を見ます。

そしてそれが0なら否定の記号、1ならそのままの形として、

それらを掛け算（AND）で結びます。

次に赤色で囲った部分を見ていきます。

同様にして0なら否定の記号、1ならそのままの形にします。

そしてそれらを掛け算（AND）で結びます。

最後に残った橙色で囲った部分を見ていきます。

これも同様の操作です。

以上の操作で得られた論理式を足し算（OR）で結びます。

これがカルノー図で簡略化した論理式となります。

＊２の累乗にあたる数以外で囲ってはダメです。

ただし１つだけ孤立している場合は囲えます。